
Previously I wrote about how I figured out how to solve the 3x3 pyramorphix.
I’ve since gotten a ShengShou gigamorphix, the 5x5 version of the puzzle. This puzzle is much more pillowed than my QiYi puzzle. The proportions of all the piece types are very different. I’m not sure how much of this is a style decision and how much is necessitated by the mechanics.
At any rate, the relationship of this puzzle to the kilomorphix is exactly the same as a 3x3x3 standard cube is to a 5x5x5 cube. You can use the same Redux method, first solving the centers, then building up the edges, then solving using regular 3x3x3 cube methods.
However, just like the differences between a cube and a pyramorphix, certain additional parities exist when solving the morphix puzzles that don’t exist with standard cubes:
- Commutator moves to build the centers actually affect 3 center pieces
- The algorithm to unflip edges in 4x4x4 and larger standard cubes rearrange solved centers
These moves actually have the same effects on standard cubes, but we don’t notice or care, because each piece looks the same as the other pieces in a solved center or edge.
Solving the Last Center
Start the Redux method by solving the centers, watching the slant of the edge pieces as well as color. Important: solve the centers one at a time, always making the center face being solved the Up face.
This method works until you have one unsolved center. When you apply the commutator algorithms, the targeted piece on the Up face doesn’t swap with the corresponding Front piece. Instead, the displaced Up face moves to the piece counterclockwise from the Front piece. (Or clockwise, if you use U instead of U’ first in your commutator.) So an edge commutator actually changes 3 edge pieces, 1 on Up and 2 on Front, and a corner commutator changes 3 corners, 1 on Up and 2 on Front.
These easiest way to use this to solve your last center is to keep that face Front. Choose the piece on the Front face you need to replace, then match the piece in the same position (edge or center) one clockwise rotation to an identical piece (color and slant) on the Up face.
You may need to do this move more than once to fix all the pieces. For the two-color corners, you may also need to move one temporarily to another face. However, most of the moves won’t require changing the solution of the Up face, although you may need to move to another face to the Up position.
The diagrams below show the two commutator algorithms needed to solve the 3x3 centers. The puzzle’s edge pieces and corners aren’t pictured, but the notation uses 5x5x5 numbering.
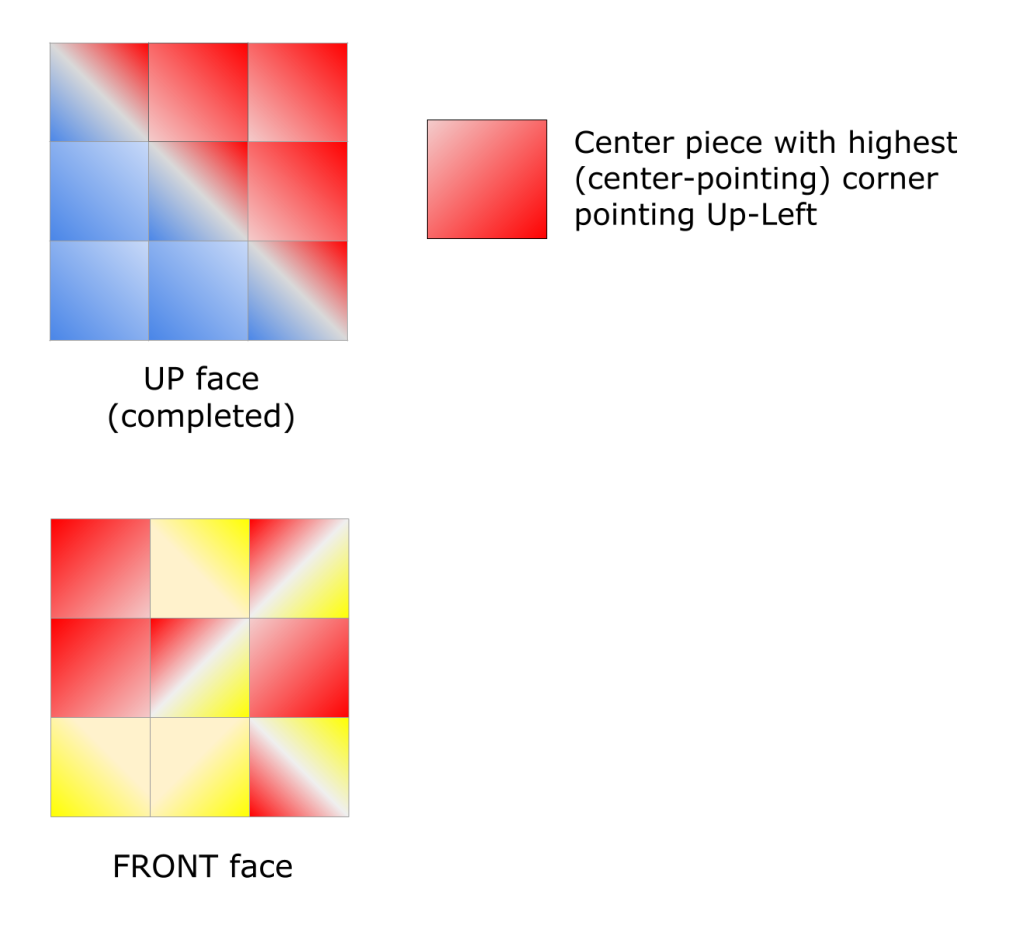
Starting position of the 3x3 puzzle centers, showing the slant of pieces as light->dark as highest->lowest. Non-center edge and corner pieces of the 5x5 puzzle are not shown.
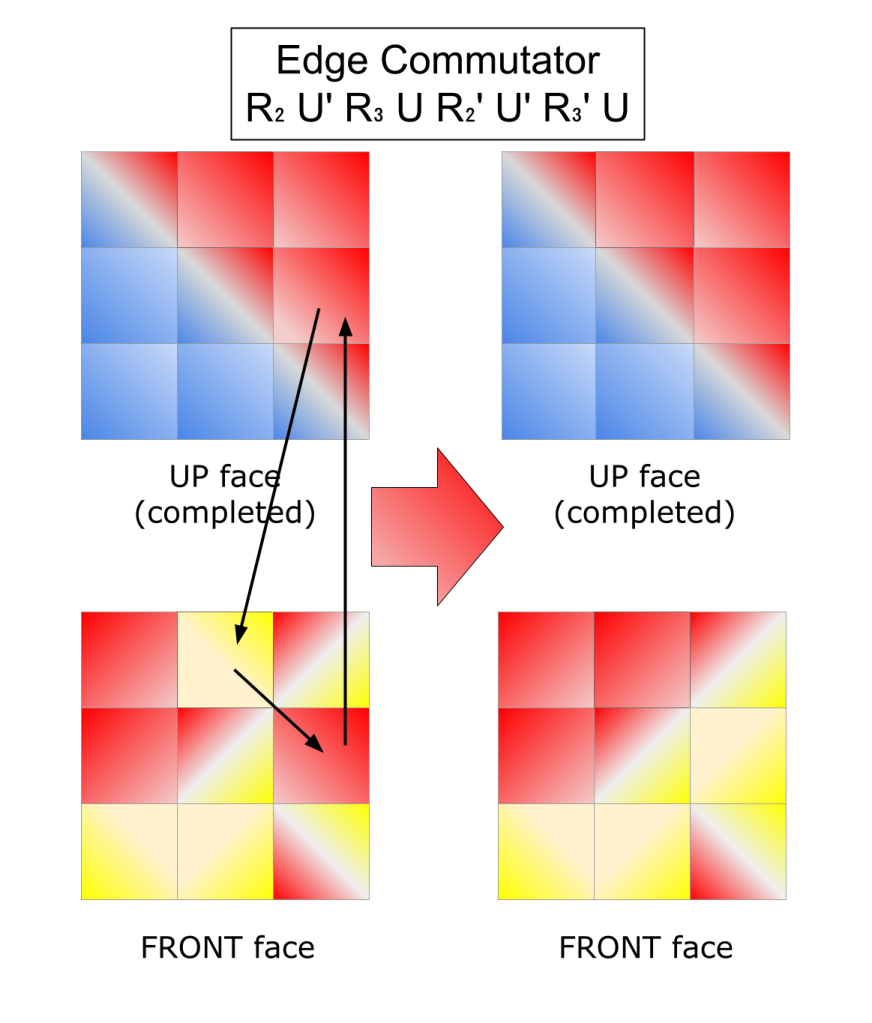
Edge commutator and effects for 3x3 puzzle centers. Non-center edge and corner pieces of the 5x5 puzzle are not shown.
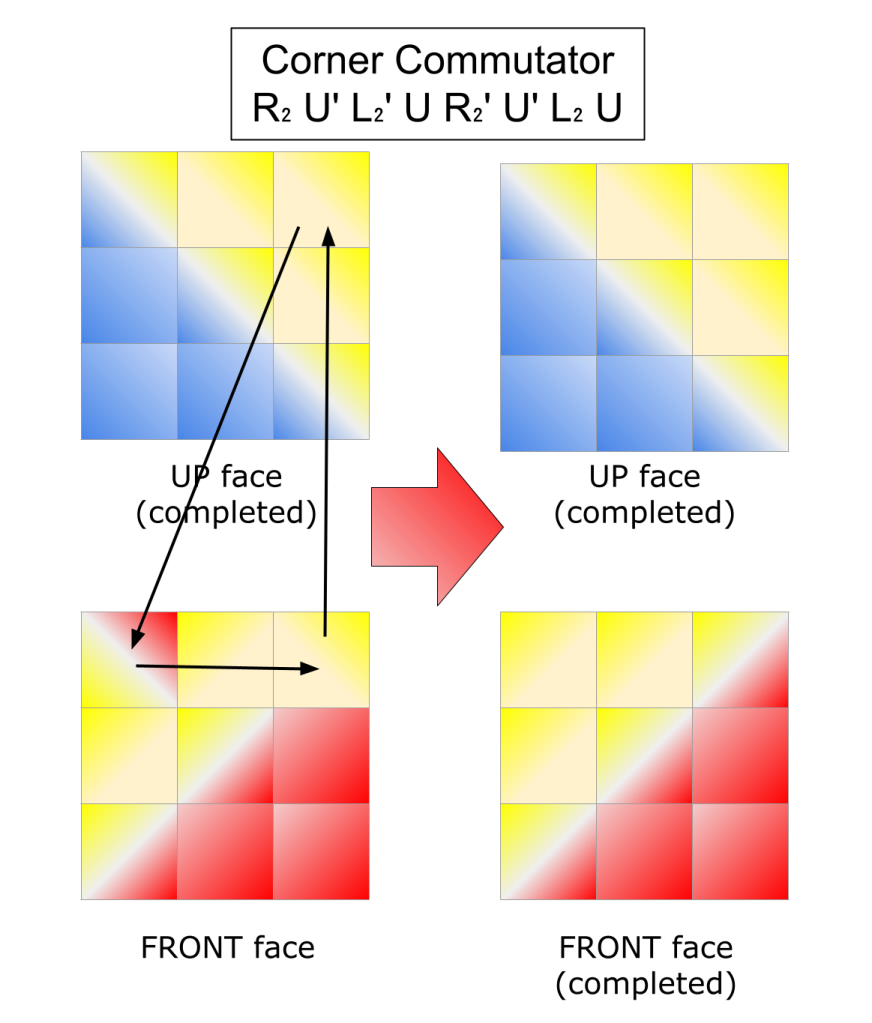
Center commutator and effects for 3x3 puzzle centers. Non-center edge and corner pieces of the 5x5 puzzle are not shown.
Solve Last Edge
If you have one last unsolved edge with the top and bottom swapped, you can just use the standard edge swap algorithms against a solved edge of the same color. While the centers of the gigamorphix take more effort than the centers of a 5x5x5 cube, the edges are easier because you have 3 sets of pieces for each color which are interchangeable.
